本篇文章由 VeriMake 旧版论坛中备份出的原帖的 Markdown 源码生成
原帖标题为:R 语言 | 基本数据类型
原帖网址为:https://verimake.com/topics/218 (旧版论坛网址,已失效)
原帖作者为:dawdler(旧版论坛 id = 64,注册于 2020-08-17 14:01:22)
原帖由作者初次发表于 2021-05-25 21:21:48,最后编辑于 2021-05-25 21:21:48(编辑时间可能不准确)
截至 2021-12-18 14:27:30 备份数据库时,原帖已获得 417 次浏览、0 个点赞、0 条回复
R语言
1. 数据类型
数据类型指的是用于声明不同类型的变量或函数的一个广泛总称,不同类型的变量将决定其占用的存储空间以及如何解释其存储的位模式。
R语言中的数据类型可以被分为最基本的三类:
· 数字
· 文本
· 逻辑
1.1 逻辑型
逻辑型变量也就是我们常说的布尔变量(Boolean),常量值只有TRUE和FALSE,注意要全大写~
1.2 文本型
1.2.1 字符串
文本型变量,即字符串,在R语言中可以使用一对单引号''或一对双引号""来表示。单引号中可以包含双引号,双引号中也可以包含单引号,但它们都不能包含自身。
注意:在R语言中,定义变量不需要声明变量类型,直接赋值即可。
##strings
a <- 'hello'
b <- "hello"
c <- 'say, "hello" '
d <- "say, 'hello' "
以上代码输出结果为:
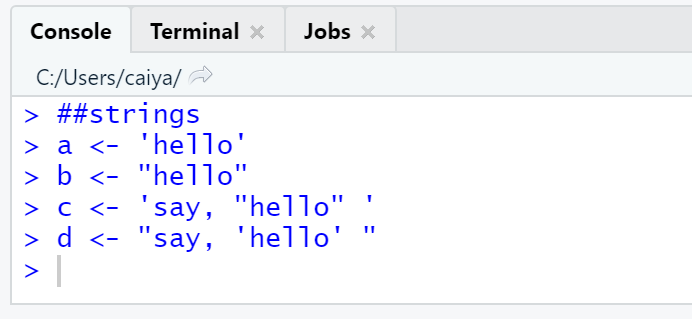
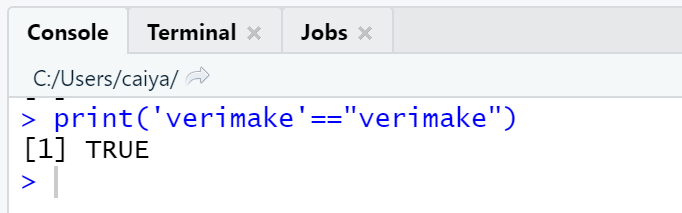
而且只要字符串内容相同,用单引号或双引号括出是等价的:
1.2.2 常用函数
以下是一些R语言中常用的对字符串进行操作的内置函数:
#common functions
#case change
print(toupper("Verimake")) #转换为全大写
print(tolower("VeriMake")) #转换为全小写
#size and length
print(nchar("verimake", type="bytes")) #显示字节数
print(nchar("verimake", type="char")) #显示字符数
#truncation
#注意:R语言中index从左往右是从1开始,不是0哦
print(substr("12345678",2,7)) #按位置,截取中间一部分
print(substring("12345678",5)) #从某位开始截取到最后
#cast
print(as.numeric("1234")) #字符串转换为数字
print(as.character(12.34)) #数字转换为字符串
#split
print(strsplit("2021/01/01", "/")) #以“/”符号为分隔符
#joint
print(paste("2021","01","01",sep="/",collapse=NULL)) #用“/”连接三段字符
print(paste(letters[1:6],1:6,sep="-",collapse="//")) #用“-”分别连接数字和字母,两两一组,每组之间用“//”分隔
#replace
print(gsub("/","-","2021/01/01")) #用“-”替代“/”
#format
#格式化输出
print(format(13.7,width=6)) #一共空出6个字符位,默认右对齐
#left justifying
print(format("verimake",width=12,justify="l")) #左对齐
#center justifying
print(format("verimake",width=12,justify="c")) #中央对齐
以上代码的输出结果为:

1.3 数字型
数字型又可以被分为数字(Numeric),整型(Integer),复合型(Complex)等,

在R语言中,我们也可以借助``函数来显示
#type of variables
var_x <- 518
print(class(var_x))
var_x <- 518L
print(class(var_x))
var_x <- "hello"
print(class(var_x))
以上代码的运行结果为:

在这基础上,我们又可以按对象类型分出六种:
**· vector** 向量
**· list** 列表
**· matrix** 矩阵
**· array** 数组
**· factor** 因子
**· data.frame** 数据框
下面先简单介绍一下向量,其他几个类型会在后面单独开出版面来具体说明~
1.3.1 向量
c()是R语言中最基本的、创造向量的一个函数,其中元素可以为文本型、逻辑型和数字型,其中数字型运用最广泛。在构成了向量的基础上,我们又可以运用运算符或内置函数对其进行一些操作:
##vectors
#create a vector
#index from 1, not 0
a = c(10, 20, 30, 40, 50) #一个变量名为a的五维数组
#taking elements
print(a[2]) #输出a的第2位
print(a[c(1,3,5)]) #取出第1、3、5项
#removing elements
print(a[c(-1,-5)]) #去掉第1和5项
#scalar computing
print(c(10, 20, 30, 40, 50)+5) #标量计算,每项加5
print(c(10, 20, 30, 40, 50)^2) #标量计算,每项计算平方
#logical computing
b = a > 20 #
print(b) #将a中的每项与20进行比较,大于则输出TRUE,小于或等于则输出FALSE
#which() is to screen elements, returning positions
#筛选出符合条件的元素,返回元素在向量中的位置
print(which(b))
print(b[which(b)])
print(a[which(b)])
#sorting
b = c(12,5,6,8,20)
print(sort(b)) #从小到大排列
print(rev(b)) #倒转向量
#return the position of ordered elements in original vector
print(order(b)) #原向量中每个元素在排序后的位置
#return the ranked position of original elements
print(rank(b)) #排序后每个元素在原向量中的位置
#vectors like c(TRUE,0) will be cast as integer combination, c(1,0)
#逻辑型和数字在同一个向量中出现的时候,逻辑型会被强制转换为数字
#NA and NULL
#NA means "deficiency", like a placeholder
#NULL means "inexistence"
print(length(c(NA,NA,NULL))) #NA 意为缺失,保留位置
print(c(NA,NA,NULL,NA)) #NULL意为不存在,不保留位置
以上代码输出结果为:


注意:如果维度不同,比如将一个二维向量与一个三维向量相加,程序不会停止运行,但这样的计算没有数学意义,会被程序警告。
1.3.2 矩阵
矩阵常见于线性代数的研究,结构类似于一个其它语言中的二维数组。一个m x n的矩阵就是一个由m行 n列(m rows x n columns)元素排列组成的矩形阵列。
R语言中创建矩阵的基本语法为:
matrix(data=NA, nrow=1, ncol=1, byrow=TRUE, dimnames=NULL) , 其中
data=NA常用一个向量将所有放于矩阵中的元素列出,
nrow表示行数,ncol表示列数,
byrow=TRUE表示按行排列,byrow=FALSE表示按列排列,按行排列即按行从左至右将向量中的元素填入,
dimnames设置行列名称
##matrix
#创建一个2行3列按行填入的矩阵
print(matrix(c(1,2,3,4,5,6),nrow=2,ncol=3,byrow=TRUE))
#创建一个3行2列按列填入的矩阵
print(matrix(c(1,2,3,4,5,6),3,2,byrow=FALSE))
#elements
m = matrix(c(4,6,7,3,5,1),nrow=2,ncol=3,byrow=TRUE)
print(m) #输出整个矩阵
print(m[1,1]) #输出第一行第一列的元素
print(m[1,3]) #输出第一行第三列的元素
#labels
colnames(m) = c("x","y","z") #从左至右设置列的名称
rownames(m) = c("a","b") #从上至下设置行的名称
print(m)
print(m["a",]) #输出“a”这一行
以上代码输出结果为:
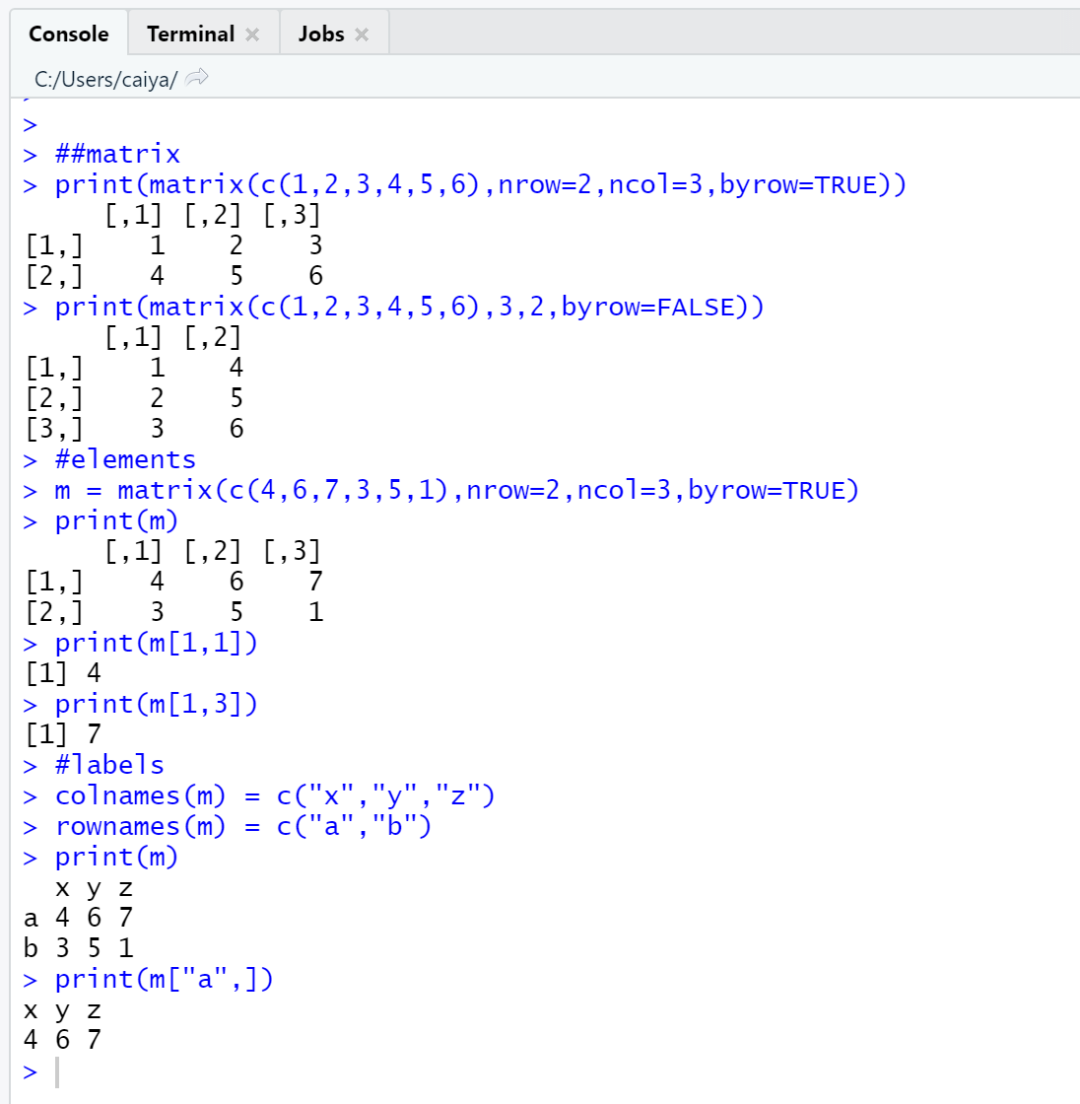
除了这些,根据矩阵本身在线性代数中的运用,还有几个基本的内置函数:
m = matrix(c(2,4,6,8,10,12), nrow=2, ncol=3, byrow=TRUE)
#transpose
print(m) #原矩阵
print(t(m)) #转置矩阵
#inverse
#must be a square matrix
#只有行列数相同,才有可能生成逆矩阵
n = matrix(c(2,4,6,8), nrow=2, ncol=2, byrow=TRUE)
print(solve(n)) #逆矩阵
#apply
#second parameter = 1: by row
print(apply(n,1,sum)) #按行求和
#second parameter = 2: by column
print(apply(n,2,sum)) #按列求和
以上代码的运行结果为:
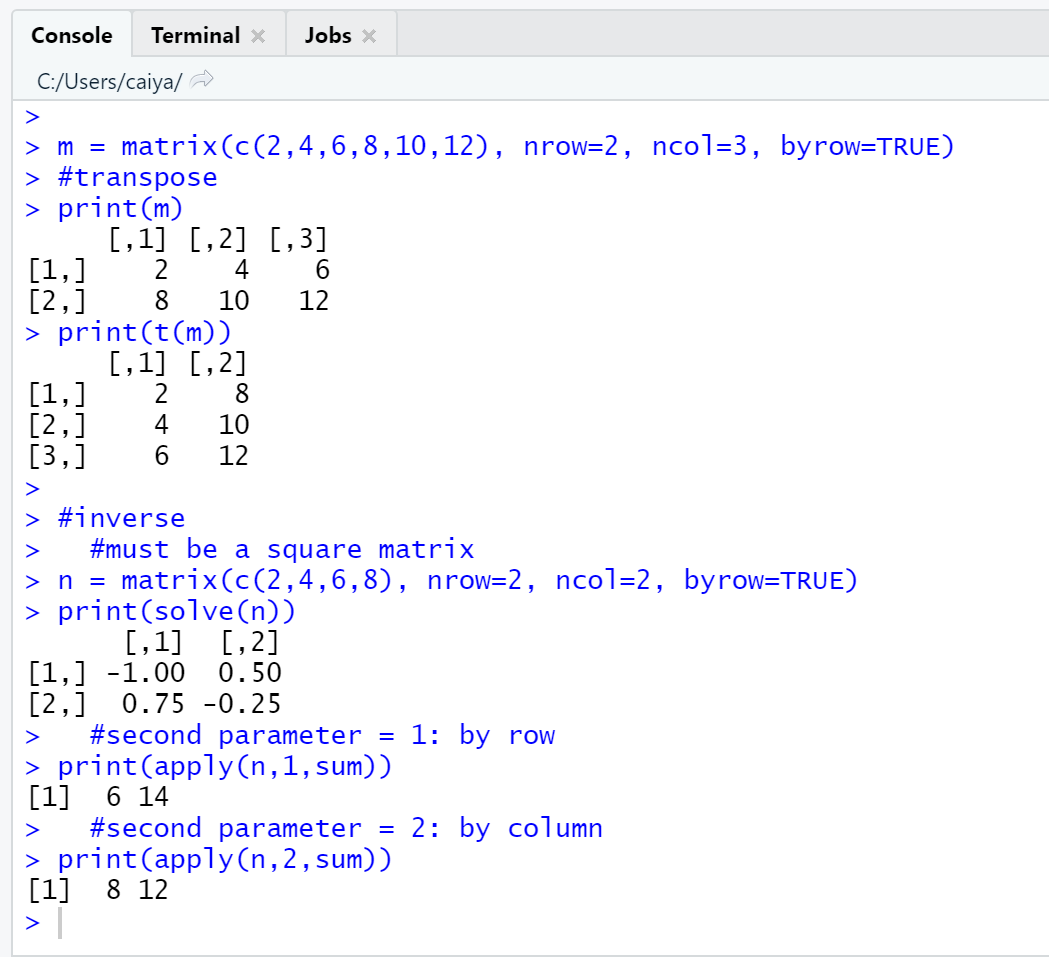
对于矩阵的计算,我们需要遵循的一个原则是,行列数分别相同的矩阵之间可以相互加减,即m x n矩阵 + m x n矩阵,并对每个位置上的元素分别做加减法;第一个矩阵的列数和第二个矩阵的行数相等的两个矩阵可以向乘,即m x n矩阵 * n x r矩阵。
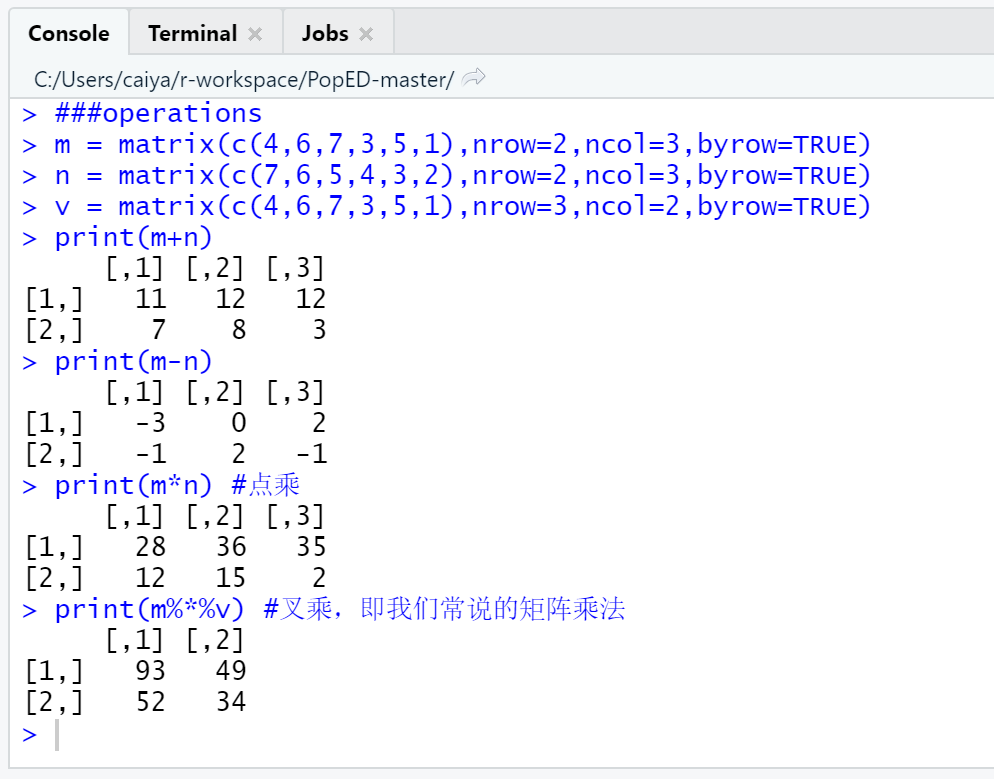
###operations
m = matrix(c(4,6,7,3,5,1),nrow=2,ncol=3,byrow=TRUE)
n = matrix(c(7,6,5,4,3,2),nrow=2,ncol=3,byrow=TRUE)
v = matrix(c(4,6,7,3,5,1),nrow=3,ncol=2,byrow=TRUE)
print(m+n)
print(m-n)
print(m*n) #点乘
print(m%*%v) #叉乘,即我们常说的矩阵乘法
以上代码的输出结果为:
最基本的关于数据类型的内容就差不多啦,下一期讲运算符~
相关资源:
https://www.runoob.com/r/r-data-types.html
https://www.runoob.com/r/r-string.html
https://www.runoob.com/r/r-matrix.html
 网站备案号:ICP备16046599号-1
网站备案号:ICP备16046599号-1