前言
本文档为2021年FPGA创新设计竞赛紫光同创杯编写的参考案例。意在辅助同学们了解整个开发平台的架构和开发方式,以在此基础上设计出更棒的参赛作品!
辅助资料
开发必备硬件工具:
PGL12G开发板x1
开发必备软件工具:
Pango Design Suite
Modelsim
原始工程样例代码(文件夹名称):
uart_test_ann
系统总体架构介绍:
单个神经元结构:

整体神经网络结构:

说明:
1、通常一个神经网络由一个input layer,多个hidden layer和一个output layer构成。
2、图中圆圈可以视为一个神经元(又可以称为感知器)
3、设计神经网络的重要工作是设计hidden layer,及神经元之间的权重
Python神经网络训练及参数导出
下载pycharm软件
下载地址:https://www.jetbrains.com/pycharm/download/#section=windows ,推荐下载community版本。
安装所需要的python库
sklearn是scikit-learn的简称,是一个基于Python的第三方模块。sklearn库集成了一些常用的机器学习方法,在进行机器学习任务时,并不需要实现算法,只需要简单的调用sklearn库中提供的模块就能完成大多数的机器学习任务。
sklearn库是在Numpy、Scipy和matplotlib的基础上开发而成的,因此在介绍sklearn的安装前,需要先安装这些依赖库。
Numpy库:Numpy(Numerical Python的缩写)是一个开源的Python科学计算库.
Scipy库:是sklearn库的基础,它是基于Numpy的一个集成了多种数学算法和函数的Python模块。
matplotlib库: 是基于Numpy的一套Python工具包,它提供了大量的数据绘图工具。
安装顺序如下所示:
1.Numpy库:
2.Scipy库:
3.matplotlib库:
4.sklearn库:
在pycharm中安装python库:
首先打开pycharm工具,选择File中的Setting选项,如下图所示
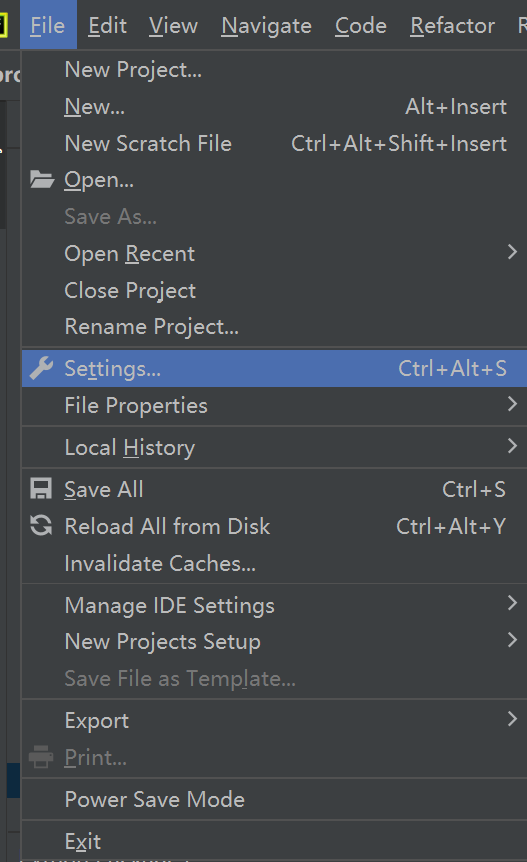
在打开的setting界面中我们点击python的解释器,你会看到很多导入的第三方库,如下图所示,点击最右边的加号
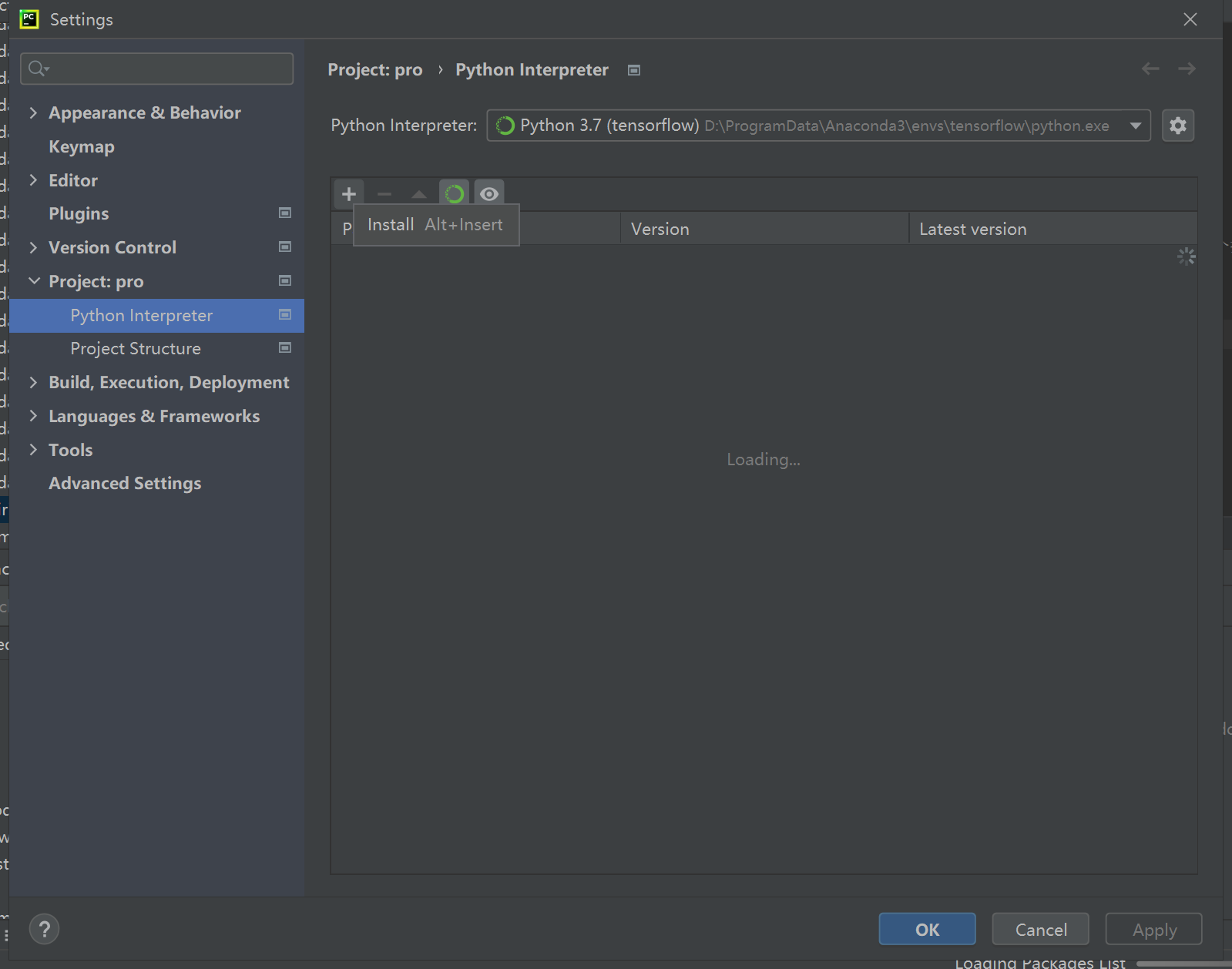
在弹出的available packages界面中,你会看到一个搜索框。然后我们搜索一个插件,比如我搜索numpy这个插件,会出现如下图所示的界面
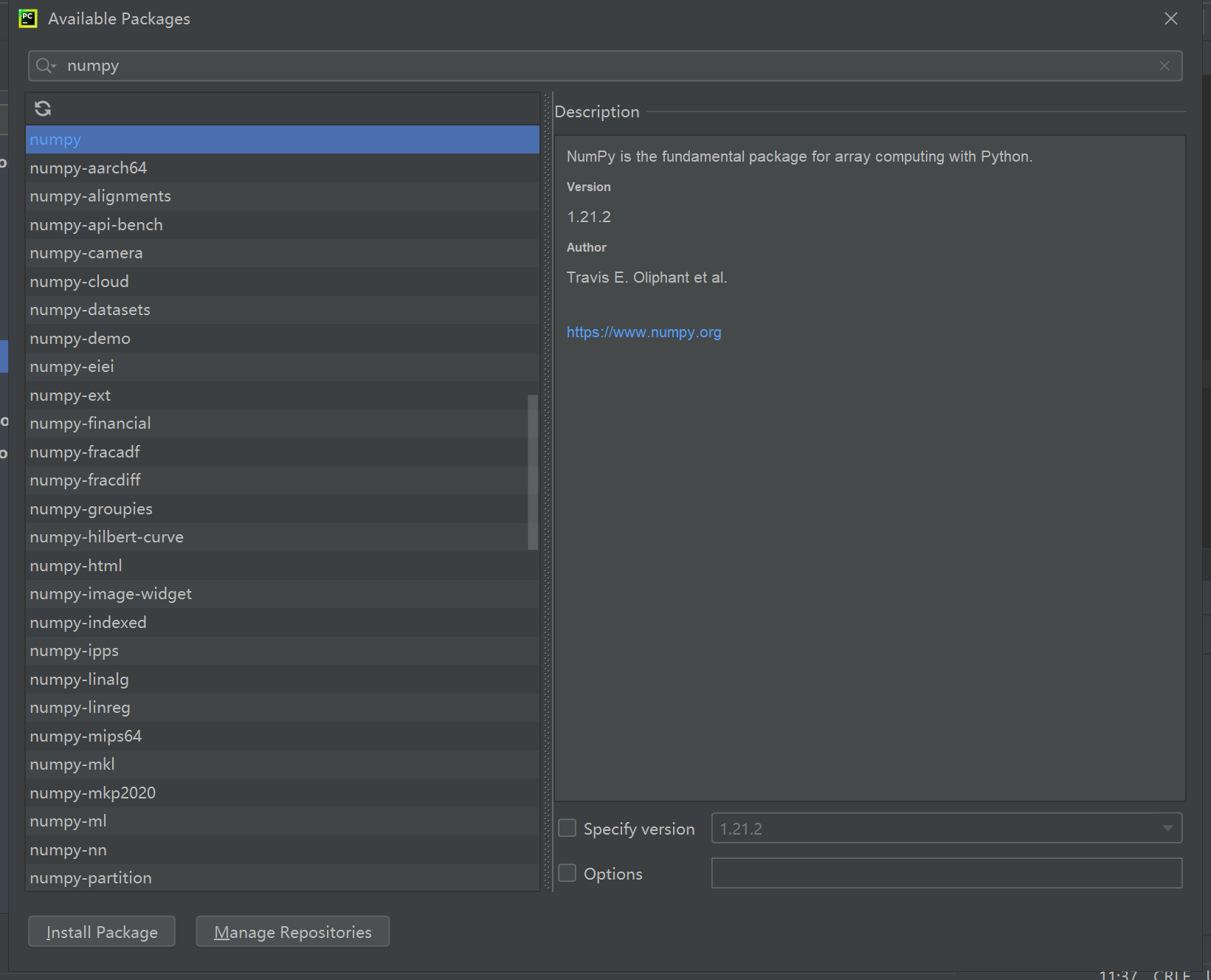
最后点击安装
进行训练
调用相关的python库
from sklearn import datasets # 加载数据集
import numpy as np # 数据处理工具
from sklearn.neural_network import MLPClassifier # 导入神经网络
调用iris训练集
iris=datasets.load_iris()
iris_x=iris.data # 属性
iris_y=iris.target # 标签
indices = np.random.permutation(len(iris_x)) # 随机产生一个序列,或是返回一个排列范围,为拆分数据做准备
iris_x_train = iris_x[indices[:-10]]
iris_y_train = iris_y[indices[:-10]]
iris_x_test = iris_x[indices[-10:]]
iris_y_test = iris_y[indices[-10:]]
把iris数据集的后10组数据作为测试集,其它组数据作为训练集
调用分类函数
在 Scikit 中神经网络被称为多层感知器(Multi-layer Perceptron),它可以用于分类或回归的非线性函数。用于分类的模块是 MLPClassifier,而用于回归的模块则是 MLPRegressor。
MLPClassifier 主要用来做分类,我们用 MLPClassifier 在鸢尾花数据上做测试。
本次示例使用的是2层隐藏层,每层8个神经元。
clf = MLPClassifier(solver='lbfgs', alpha=1e-5,
hidden_layer_sizes=(8, 8), random_state=1)
clf.fit(iris_x_train,iris_y_train) #拟合
iris_y_predict = clf.predict(iris_x_test)
score=clf.score(iris_x_test,iris_y_test,sample_weight=None)
训练结果
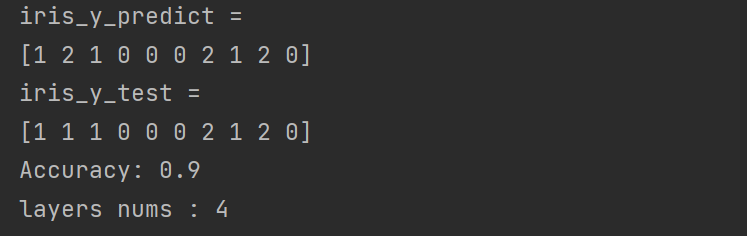
参数导出
MLPClassifier 属性说明:
- classes:每个输出的类标签
- loss:损失函数计算出来的当前损失值
- coefs:列表中的第i个元素表示i层的权重矩阵
- intercepts:列表中第i个元素代表i+1层的偏差向量
- n_iter :迭代次数
- n_layers:层数
- n_outputs:输出的个数
- out_activation:输出激活函数的名称。
我们本次使用- coefs 、- intercepts来导出我们所需要的权重和偏差参数
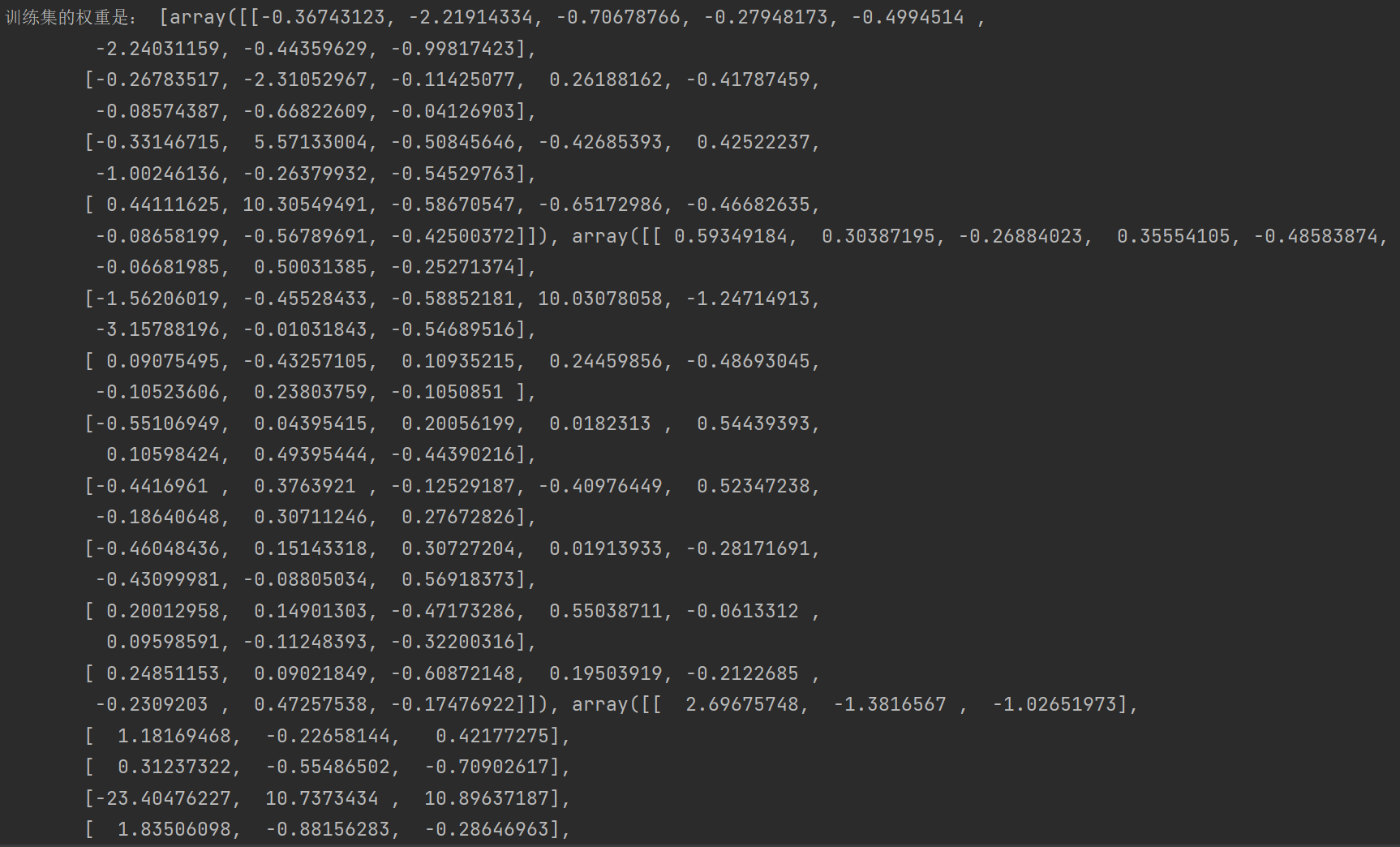
print ('训练集的权重是:', clf.coefs_)
print('训练集的偏差是:', clf.intercepts_)
参数提取结果
RTL级ANN神经网络的实现
参数定义
因为训练得到的参数结果都是浮点数,所以我们需要先把它转换成定点数
本次示例采用的是21位定点数,一位符号位,八位整数位,十二位小数位。
parameter w1_1 = 21'b1_1111_1111_1010_0001_1011;
parameter w2_1 = 21'b1_1111_1101_1100_0011_1110;
parameter w3_1 = 21'b1_1111_1111_0100_1011_0010;
parameter w4_1 = 21'b1_1111_1111_1011_1000_1000;
parameter w5_1 = 21'b1_1111_1111_1000_0000_0011;
parameter w6_1 = 21'b1_1111_1101_1100_0000_1001;
parameter w7_1 = 21'b1_1111_1111_1000_1110_1000;
parameter w8_1 = 21'b1_1111_1110_1111_1111_1001;
单个神经元的代码实现
乘累加运算:
always @(posedge clk or negedge rst_n) begin
if (!rst_n) begin
sum1_1 = 41'd0;
sum_1 = 21'd0;
sum2_1 = 21'd0;
end
else begin
sum1_1 = in1 * w1;
sum2_1 = {sum1_1[40],sum1_1[31:24],sum1_1[23:12]};
sum_1 =sum_1 +sum2_1;
end
end
乘累加的结果加上偏差:
else if (cnt_1 == 8'd6) begin
suma<= sum_1+b1;
sumb<= sum_2+b2;
sumc<= sum_3+b3;
sumd<= sum_4+b4;
sume<= sum_5+b5;
sumf<= sum_6+b6;
sumg<= sum_7+b7;
sumh<= sum_8+b8;
end
Relu激活函数的实现:
assign suma1 = (suma[20] == 1'd0 )? suma: 21'b0;
assign sumb1 = (sumb[20] == 1'd0 )? sumb: 21'b0;
assign sumc1 = (sumc[20] == 1'd0 )? sumc: 21'b0;
assign sumd1 = (sumd[20] == 1'd0 )? sumd: 21'b0;
assign sume1 = (sume[20] == 1'd0 )? sume: 21'b0;
assign sumf1 = (sumf[20] == 1'd0 )? sumf: 21'b0;
assign sumg1 = (sumg[20] == 1'd0 )? sumg: 21'b0;
assign sumh1 = (sumh[20] == 1'd0 )? sumh: 21'b0;
资源复用设计
因为每层的神经元的运算内容是一样,所以我们可以通过复用神经元来减少对资源的使用
本次示例通过改变每个神经元的输入和参数,来进行对神经元的复用,然后通过计数器来计算在每一层运算的时间,当到达了规定的时间就取出现应的结果,然后进行下一层的运算。
always @(posedge clk or negedge rst_n) begin
if (!rst_n) begin
cnt_1<= 8'd0;
cnt_2<= 8'd0;
cnt_3<= 8'd0;
end
else if(valid_in == 1'd1) begin
cnt_1 <= cnt_1 + 1'd1;
if(cnt_1>=8'd6 && cnt_3 <=8'd20)
cnt_2 <=cnt_2 + 1'd1;
if(cnt_2 >= 8'd10 && cnt_3 <=8'd20)
cnt_3<=cnt_3 + 1'd1;
if(cnt_3 ==8'd20)begin
cnt_1<= cnt_1;
cnt_2<=cnt_2 ;
cnt_3<= cnt_3;
end
end
else if (cnt_1 == 8'd6) begin
suma<= sum_1+b1;
sumb<= sum_2+b2;
sumc<= sum_3+b3;
sumd<= sum_4+b4;
sume<= sum_5+b5;
sumf<= sum_6+b6;
sumg<= sum_7+b7;
sumh<= sum_8+b8;
end
else if (cnt_2 == 8'd10) begin
suma_1<= sum_1+b1;
sumb_1<= sum_2+b2;
sumc_1<= sum_3+b3;
sumd_1<= sum_4+b4;
sume_1<= sum_5+b5;
sumf_1<= sum_6+b6;
sumg_1<= sum_7+b7;
sumh_1<= sum_8+b8;
end
else if (cnt_3 == 8'd10) begin
out1<= sum_1+b1;
out2<= sum_2+b2;
out3<= sum_3+b3;
end
else if (cnt_1 > 8'd0&&cnt_1 <= 8'd4)begin
b1 <= b1_1;
b2 <= b2_1;
b3 <= b3_1;
b4 <= b4_1;
b5 <= b5_1;
b6 <= b6_1;
b7 <= b7_1;
b8 <= b8_1;
case(cnt_1)
8'd1: begin
in1 <= ina;
w1 <= w1_1 ;
w2 <= w2_1 ;
w3 <= w3_1 ;
w4 <= w4_1 ;
w5 <= w5_1 ;
w6 <= w6_1 ;
w7 <= w7_1 ;
w8 <= w8_1 ;
end
8'd2: begin
in1 <= inb;
w1 <= w1_2 ;
w2 <= w2_2 ;
w3 <= w3_2 ;
w4 <= w4_2 ;
w5 <= w5_2 ;
w6 <= w6_2 ;
w7 <= w7_2 ;
w8 <= w8_2 ;
end
8'd3: begin
in1 <= inc;
w1 <= w1_3 ;
w2 <= w2_3 ;
w3 <= w3_3 ;
w4 <= w4_3 ;
w5 <= w5_3 ;
w6 <= w6_3 ;
w7 <= w7_3 ;
w8 <= w8_3 ;
end
8'd4: begin
in1 <= ind;
w1 <= w1_4 ;
w2 <= w2_4 ;
w3 <= w3_4 ;
w4 <= w4_4 ;
w5 <= w5_4 ;
w6 <= w6_4 ;
w7 <= w7_4 ;
w8 <= w8_4 ;
end
default: begin
in1<=0;
w1 <= 0 ;
w2 <= 0 ;
w3 <= 0 ;
w4 <= 0 ;
w5 <= 0 ;
w6 <= 0 ;
w7 <= 0 ;
w8 <= 0 ;
end
endcase
整体实现
Modelsim仿真结果:

本次示例通过串口来验证神经网络在开发板上的准确性,结果如图:


所得的结果与训练的结果一致!
 网站备案号:ICP备16046599号-1
网站备案号:ICP备16046599号-1